Type Expression Problem#
Overview#
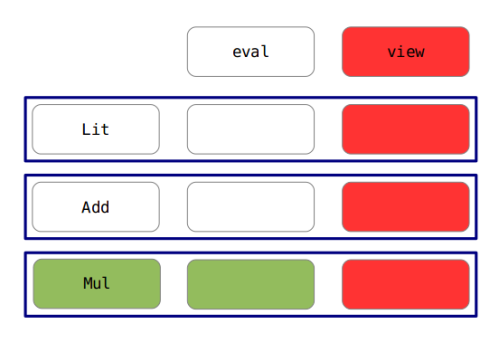
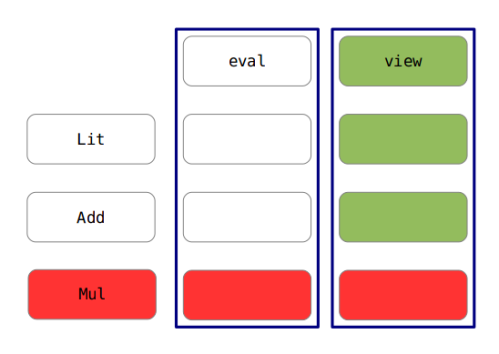
It refers to the difficulty of writing data abstractions that can be easily extended with both new operations and new data variants.
- if your abstraction is function oriented (e.g. functional languages), adding new operations (functions) is easy but adding new data variants (types) is difficult
- if your abstraction is type oriented (e.g. OOP), adding new data variants (classes) is easy but operations is difficult
Trivial Example#
Consider implementing a language for arithmetic expressions (e.g.: 1 + 2, 4 * 5, (8 + 3) * 4)
So, there is an initial set of features comprised by the initial types of expressions and operations over those expressions.
- Initial feature set
- Types of expressions: Integer literals, addition.
- Operations: Evaluation of expressions.
- Evolution 1: Add a new type of expressions. For example, subtraction.
- Evolution 2: Add a new operation. For example pretty printing.
Note that there is a lot more that can be done in terms of evolution, but those two basic evolutions serve to illustrate the essence of the problem.
Requirements for a solution#
- Extensibility in both dimensions: A solution must allow the addition of new data variants and new operations and support extending existing operations
- Strong static type safety: A solution must prevent applying an operation to a data variant which it cannot handle using static checks
- No modification or duplication: Existing code must not be modified nor duplicated
- Separate compilation and type-checking: Safety checks or compilation steps must not be deferred until link or runtime
- Independent extensibility: It should be possible to combine independently developed extensions so that they can be used jointly
Expression Problem: another formulation https://oleksandrmanzyuk.wordpress.com/2014/06/18/from-object-algebras-to-finally-tagless-interpreters-2/
Object Algebras#
We begin again by considering the language containing only literals and addition. It is going to be described by an interface
interface ExpAlg<T> {
T lit(int n);
T add(T x, T y);
}
- similar to Visitor interface.
- key difference: interface is going to play a completely different role.
ExpAlg<T>is an interface of an abstract factory for creating expressions.
For example, the expression (1 + (2 + 3)) is represented as follows
<T> T e1(ExpAlg<T> f) {
return f.add(
f.lit(1),
f.add(
f.lit(2),
f.lit(3)));
}
it is represented as a function taking as an argument an object f implementing the interface ExpAlg<T> (i.e., a concrete factory) and returning a value of type T. The body of the function simply calls the methods lit and add of the factory f in a suitable order with suitable arguments.
This representation allows us to vary the concrete factory f thus interpreting the expression e1 in different ways.
Let us see how this works in the case of evaluation of expressions.
First of all, we introduce an interface Eval of “objects that can be evaluated”:
interface Eval { int eval(); }
Next we define a concrete factory EvalExp, which is going to manufacture expression that can be evaluated:
class EvalExp implements ExpAlg<Eval> {
Eval lit(final int n) {
return new Eval() {
int eval() {
return n;
}
};
}
Eval add(final Eval x, final Eval y) {
return new Eval() {
int eval() {
return x.eval() + y.eval();
}
};
}
}
let us think how we could add multiplication to our language.
We could add a new method mul to the interface ExpAlg<T>, but then the implementation of the concrete factory EvalExp would require changes, which is precisely what we would like to avoid.
Instead, we introduce a new interface MulAlg<T> that extends the interface ExpAlg<T> and adds a new method mul to it:
interface MulAlg<T> extends ExpAlg<T> {
T mul(T x, T y);
}
Expressions containing multiplication are now going to be represented as functions taking as an argument objects implementing the extended interface MulAlg<T>. For example, the expression (4 * (5 + 6)) will be represented as follows:
<T> T e2(MulAlg<T> f) {
return f.mul(
f.lit(4),
f.add(
f.lit(5),
f.lit(6)));
}
To extend the implementation of evaluation of expressions to expressions containing multiplication we define a new concrete factory EvalMul that implements the interface MulAlg<Eval> and inherits from the factory EvalExp implementations of the methods lit and add:
class EvalMul extends EvalExp implements MulAlg<Eval> {
Eval mul(final Eval x, final Eval y) {
return new Eval() {
int eval() {
return x.eval() * y.eval();
}
};
}
}
We can now pass an instance of the factory EvalMul into the expression e2, get back an object that can be evaluated, and compute its value by calling the eval method:
int v2 = e2(new EvalMul()).eval();
Note that we are not touching any existing code: we are defining new interfaces and classes and use inheritance to avoid duplication.